The Curry-Howard Square
While trying to better understand categorical diagrams, I tried to map out some familiar (to me) concepts; I conclude by discussing how effective semantics is related.
What Is Curry-Howard?
The Curry-Howard correspondence says that proof and computation are the same thing – often expressed as “types are theorems” and “functions are proofs”.
I’d suggest reading the Wikipedia entry on the topic, if you’re unfamiliar. This post largely builds on those ideas and expresses them in a way I found insightful.
What Is The Curry-Howard Square?
While trying to better understand effective semantics of software, I drew this diagram.
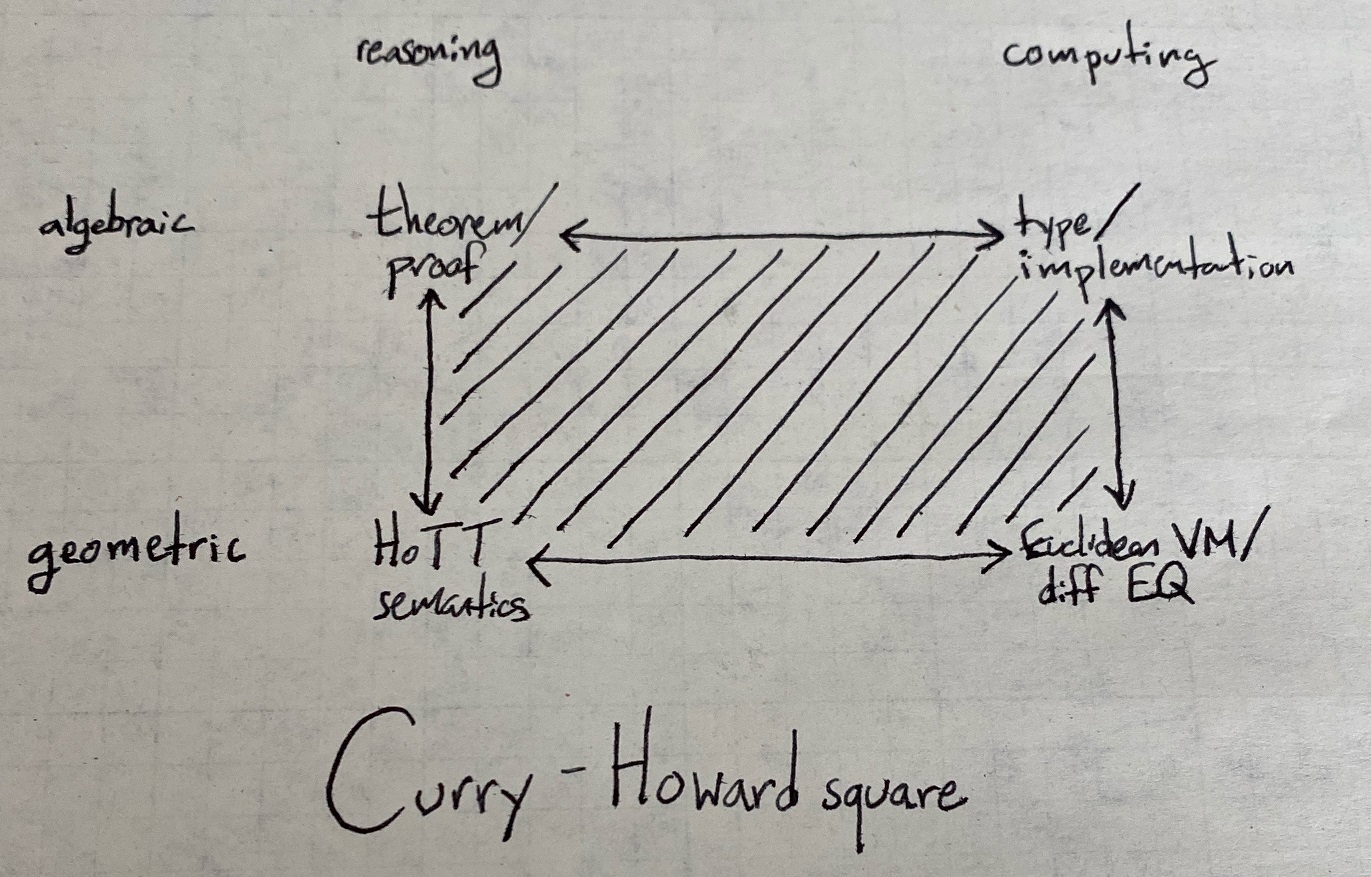
This square represents two-dimensions of equivalence:
- The correspondence between reasoning and computing (Curry-Howard) along the horizontal axis.
- The correspondence between algebra and geometry along the veritcal axis.
On the far left is the correspondence between type theory and category theory, as different expressions of logic. On the far right is the correspondence between programs defined in a language and programs defined by their execution behavior on, eg, Euclidean VMs.
We can think of things that are perhaps not one of the corners:
- software which reasons about software is along the top edge; or,
- machine learning models are along the right edge – definitions of the difference equations to run on sections of a machine, via the language.
How Is Effective Semantics Related?
Effective semantics is a research program to find pathways from the bottom-right corner (the world of difference equations on machines) to the top-left corner (the world of type theory and languages).
My plan is two parts:
- Make the journey in reverse, starting at the top-left (type theories) and mapping them to the bottom-right (difference equations). This direction is well researched. My goal is implementing challenge problems in formal verification within the math community, eg, verifying Brunerie’s number is 2.
- Once I’ve implemented that direction, use that path as inspriation for the reverse direction.
My current thinking is to first make the transition from computation to reasoning via topological analysis and categorification, and then the transition from geometric to algebraic by finding a matching type theory which describes the effective semantics of the computing system. There has been recent work in the math community to construct canonical type theories from a given semantic model.
This extracted language would be the internal language of a machine learning model – and I believe the development of an artificial intelligence capable of reasoning deductively in its internal language is a key step to full artificial intelligence.
 Z. Michael Gehlke
Z. Michael Gehlke